I confess to being fascinated by Taylor Swift for far more than her music. I think she is an extraordinary person for her philanthropy, her speaking out for victims of sexual assault, her advocacy of artists' ownership rights, and her urging her fans to vote.
But of course there's much more, and so let's look at the mathematics of Taylor Swift.
Let's start with her net worth. She is estimared to have $1.6 billion in assets. Her largest asset is her music catalog. She did not own the masters (first recording) to her older music, but she re-recorded them and owns the masters to the re-recorded versions and to her future recordings.
She donates large sums to a variety of organizations. Most of these donations are not public, but here is a sample of some recent donations:
There are three parts to this mathematical analysis:
1.
her attractiveness,
2.
her lipstick shades, and
3.
her lyrics.
Each part contains a considerable amount of imprecision in measuremenys and judgments. This is more of a work in progress than the final word. Nevertheless, I think it is a non-routine use of math, and it was a lot of fun.
1. How pretty is she?
You can have your opinion. But mine is based on math.
The ancient Greeks discovered a particular number called the Golden Ratio, denoted by Greek letter Φ (phi), that has many interesting mathematical properties, apppears
in some patterns of nature, and is considered by many to be asthetically pleasing. The Golden Ratio results from finding the point on a line segment that splits the segement into two smaller segments with lengths a and b, such that (a + b)/a = a/b.
That ratio a/b is the Golden Ratio, Φ. With a little algebra, Φ = (1 + √5)/2 , which is an irrational number so it has an infinite non-repeating decimal, and rounded to three decimal places is 1.618.
Renaissance artists, plastic surgeons, and makeup artists are among those who use Golden Ratios in various ways with faces to create ideally proportioned faces. Gary Meisner has wriiren extensively on the Golden Ratio, and he believes there are over 20 different ways that the Golden Ratio shows up in human faces and that “the Golden Ratio is also found very commonly in beautiful models of today across all ethnic groups". Biostatistican professor Dr. Kendra Schmid and her colleagues performed various measures of many faces. They began with 17 potential Golden Ratios, and they decided only six of these ratios were predictors of facial attractiveness. See
Schmid.
This takes us to Taylor. I attempted to measure these six ratios on a picture of Taylor. There are many pictures of her, she does enjoy experimenting with different hairstyles, and I had to find one with a hairstyle that gave me the best chance of measuring her from her hairline and also between her ears. The measurement is not exact for many reasons, and because we are using a two-dimensional photo of a three-dimensional object there is certainly some loss of accuracy. Nevertheless, here are the results:
| Face length / Face Width | 1.4722 |
| Mouth width / Interocular distance | 1.4000 |
| Mouth width / Nose width | 1.5556 |
| Lips to chin / Interocular | 1.7000 |
| Lips to chin / Nose width | 1.8889 |
| Ear length / Nose width | 1.5556 |
| Average | 1.5954 |
| % Deviation from Φ | - 1.4% |
On average, Taylor's measurements are quite close to phi, the ideal measurement of facial attractiveness.
(Note that I did the measurements manually, and they are inexact. I understand there are Python libraries such as dlib that can detect facial ladmarks, and this might eliminate some of the imprecision.)
2. What lipstick shade is she wearing?
A common question on the Internet is what are her favorite lipsticks. I think more interesting mathematically is: given a particular photo of Taylor, can we get the computer to mathematically identify her lipstick?
First, a little background about image files on the computer. A computer image is a collection of tiny dots called pixels. Each dot is about 1/96 inch.
Each pixel contains a color code, as a 6-digit base 16 (hex) number, or as a 6 digit base 10 red-green-blue ordered triple.
For example 861A23 in base 16 equals (134, 26, 35) in rgb base 10. The first two hex digits, 86, is the red. 86 in base 16 equals 8*161 + 6*160 = 134 in base ten. The second two hex digits, 1A, is the green, etc.
We can ask how similar two colors are by plotting them in 3D and calculating their distance.
D = √ [ (134 – 174)2 + (26 – 31)2 + (35 – 61)2 ] = 48.0
I started with five different photos of Taylor, where it appears to me she is wearing a different shade in each. I tried to crop each photo as a rectangular area as close as I could get to just her lips, and I saved each cropped rectangle as a file. I used R packsge colouR to find the most frequent colors. This was unsatisfactory, possibly because there was too much background color noise. I found a website https://www.remove.bg/
that removes background, and I retried colouR with the background removed files.
I did the same process with online swatches of ten lipsticks that the Internet says are among Taylor's favorites.
To my surprise, there were more than 50 different colors, most of them reasonably close, on both the Taylor photos and on the lipstick swatches.
Why are there so many colors?
- there are 166 = 16,777,216 different computer colors
- women tell me lipstick never looks same on a person as in a tube
- my dermatologist offered that lips have lines and grooves that create uneven coloring
- it is hard to isolate the image of just lips in a rectangle
- lighting creates distortions
- there are image resolution and quality issues
Nevertheless, I decided to do the following. For each of Taylor's ten favorite lipsticks, I found the ten most frequent colors.
For each of the five Taylor lip photos, I found their ten most frequent colors. Then for each photo, I calculated the average color distance from the photo to each lipstick. The lipstick with the minimum distance from the photo was then the computer forecast matching a photo to a lipstick.
Get it?
Here are the five Taylor photos with the computer's match:
In summary, the computer thinks photo 1 has the minimum distance, 320, to its match. Do you agree this is the best match?
| Photo | Shade | Distance |
| 1 | Ruby Woo | 320 |
| 2 | Elson 4 | 625 |
| 3 | Blood Lust | 388 |
| 4 | Flame | 392 |
| 5 | Flame | 399 |
3. Which of her songs are emotional?
The R package ‘taylor’ contains lyrics for 11 albums and 240 songs.
I will examine TS songs for their emotional content, as follows:
- % emotional words per song
- most frequent words per song
- trend in emotions over time
- examine theory that 5th song in every album is most emotional
What makes a song emotional? Some possibilities are: emotional words, volume, tempo. pitch, rhythm, and
instrumentation. A few musicians I spoke to have a longer list. But I don't have the data to measure
any of these, except emotional words.
Linguists have created lists of emotional words. Mohammad and Turney created the
NRC Emotion Lexicon
list of over 14,000 English words and their associations with ten basic emotions (anger, anticipation, disgust, fear, joy, negative, positive, sadness, surprise, and trust). A word may have more than one emotion. For example, faith has the emotions
anticipation, joy, positive, and trust.
Like most datasets, Taylor Swift songs required a considerable amount of data cleaning. In a text analysis like this, data cleaning includes removing punctuation and capitals, deleting stop words (a, oh, the, etc.) that add no value, and fixing informal speech and
colloquialisms (dyin’, gonna, etc.). Taylor uses a large number of colloquialisms, often by dropping an ending g in an "ing" word. Also part of the cleaning is that words are stemmed so that love, lovable, loving, and lovely all reduce to "lov"; and then the stemmed words are lemmatized and returned to their root word love. The R packages SnowballC and textstem perform stemming and lemmatizing respectively. However, this combination did not always produce a valid lemmatized word, and I manually adjusted about 500 words which I placed into a file lem_replacements_df.csv. The final result is over 23,000 words from her 240 songs, which I am calling processed words.
For all 240 songs combined, I calculated Taylor's most frequent words, her most frequent emotional words, her number of words for each of the 10 emotions, and the ratio r = number of emotional words / number of processed) words. The results are contained in the following three plots:
The above is a baseline for all songs combined. The r value is .364. I asked a friend whose teen-aged daughter is a Swiftie, to suggest a few Taylor songs that she considers especially emotional, and I created the same types of plots for some of these songs. I'll share the plots for the song "My Tears Ricochet", which had a greater than average r value:
Note that in the above song, the counts are pretty small. Perhaps this is one explanation for why
a number of songs that we thought were emotional did not have a higher than average r value.
Another question I was curious about is whether Taylor's songs have become more emotional over time. I am using original release date of album as the time variable. For songs that Taylor re-recorded, I am using the original release date under the assumption that her re-release may have changed the music but not the lyrics.
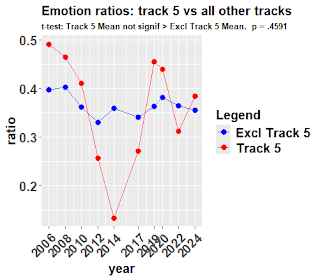
That her songs are becoming more emotional over time appears not to be true. To the contrary, the slope of a poor fitting trend line is negative, but its F-statistic says the linear model is not significant.
Finally, there is a theory that every fifth song on an album is intentionally more emotional than the others.
This
theory is discussed on the Internet and even Taylor gives it some credence. Albums by release year provide 10 data points (there are 11 albums, but two were released in the same year). In 6 years out of 10 the track 5 r ratio exceeded the all other tracks, and in 4 years out of 10 they did not.
A two-sample t-test with one tail concludes that the track 5 mean is not significantly greater than the all other tracks mean, p = .4591.
Note that track 5 has an outlier, “All you had to do was stay,” which sounds like it should have a high r, but its r was .134.
4. Bonus: &$!#%
To the Taylor Tots parents:
Our Taylor has been known to use an R-rated word in her songs, or two. Here is the frequency of some of her most frequent such words (and there are others), mostly from her Tortured Poets Department album:
As I mentioned earlier, each of the three parts of this analysis - her attractiveness, her lipstick shades, and her lyrics - contains various imprecisions and judgments. Perhaps some day I will go back to this project and make some improvements. Comments are welcome.
But I think it was a non-routine use of math. And it was fun!
This project uses three R script files and a number of image files. The R code is shown below, but it is long. Both the R code files and the image files may be found at https://github.com/fcas80/The-Taylor-Swift-Project/tree/main
# file 1 of 3: lovely.txt
library(png)
library(ggplot2)
library(grid)
image_path <- "my_path/ts1_phi_removebg.png"
img <- readPNG(image_path, native=TRUE) # width 584, height 457
height <- nrow(img) # 383
width <- ncol(img) # 331
raster_img <- grid::rasterGrob(img, interpolate = TRUE)
df <- data.frame(xpos = c(0, width), ypos = c(0, height))
# 1. plot photo on minimum grid
ggplot(data = df,
aes(xpos, ypos)) +
xlim(0, width) + ylim(0, height) +
geom_blank() +
annotation_custom(raster_img, xmin=0, xmax=width, ymin=0, ymax=height) +
theme(axis.title.x = element_blank(),
axis.title.y = element_blank())
# 2. plot photo on more detailed grid; measurements are manual and imprecise
ggplot(data = df,
aes(xpos, ypos)) +
xlim(0, width) + ylim(0, height) +
geom_blank() +
annotation_custom(raster_img, xmin=0, xmax=width, ymin=0, ymax=height) +
geom_hline(yintercept = seq(0, height, by = 10), color = "gray", linwidth = 0.5) +
geom_vline(xintercept = seq(0, width, by = 10), color = "gray", linwidth = 0.5) +
scale_x_continuous(breaks = seq(0, width, by = 20)) +
scale_y_continuous(breaks = seq(0, height, by = 20)) +
annotate("segment", x = 90, y = 265, xend = 90, yend = 0, color = "red", linwidth = 3) +
annotate("segment", x = 70, y = 90, xend = 250, yend = 90, color = "red", linwidth = 3) +
annotate("segment", x = 130, y = 170, xend = 180, yend = 170, color = "red", linwidth = 3) +
annotate("segment", x = 135, y = 105, xend = 180, yend = 105, color = "red", linwidth = 3) +
annotate("segment", x = 125, y = 70, xend = 195, yend = 70, color = "blue", linwidth = 3) +
annotate("segment", x = 160, y = 85, xend = 160, yend = 0, color = "blue", linwidth = 3) +
annotate("segment", x = 50, y = 160, xend = 50, yend = 90, color = "red", linwidth = 3) +
theme(axis.title.x = element_blank(),
axis.title.y = element_blank())
segments_df <- data.frame(
segment_name = c("face_length", "face_width", "dist_bet_eyes",
"nose_width", "mouth_width", "lips_to_chin", "ear_length"),
x = c(90, 70, 130, 135, 125, 160, 50),
y = c(265, 90, 170, 105, 70, 85, 160),
xend = c(90, 250, 180, 180, 195, 160, 50),
yend = c(0, 90, 170, 105, 70, 0, 90))
segments_df$dist <- sqrt((segments_df$x - segments_df$xend)^2 + (segments_df$y - segments_df$yend)^2)
segments_df
ratios_df <- data.frame(
ratio_name = c("face length / width", "mouth width / interocular", "mouth width / nose width",
"lips to chin / interocular", "lips to chin / nose width", "ear length / nose width"),
ratio = rep(0, times=6))
ratios_df$ratio[1] <- round(segments_df$dist[1] / segments_df$dist[2], 4) # face length / width
ratios_df$ratio[2] <- round(segments_df$dist[5] / segments_df$dist[3], 4) # mouth width / interocular
ratios_df$ratio[3] <- round(segments_df$dist[5] / segments_df$dist[4], 4) # mouth width / nose width
ratios_df$ratio[4] <- round(segments_df$dist[6] / segments_df$dist[3], 4) # lips to chin / interocular
ratios_df$ratio[5] <- round(segments_df$dist[6] / segments_df$dist[4], 4) # lips to chin / nose width
ratios_df$ratio[6] <- round(segments_df$dist[7] / segments_df$dist[4], 4) # ear length / nose width
ratios_df
m <- round(mean(ratios_df$ratio),3)
m
error <- round((m - (1+sqrt(5))/2)/m,3)
error
# END
# file 2 of 3: lipsticks.txt
setwd("my_path")
library(colouR)
library(ggplot2)
# These shades were determined from various Internet articles
shade <- c("Ruby Woo", "Morocco", "Dragon Girl", "Elson 4", "Always Red", "Kyoto Red",
"Eadie Scarlet", "Blood Lust", "Flame", "Red to Go")
# These swatches of shades were copied from various Internet stores
df_lipsticks <- data.frame(shade,
file = c("Mac_Ruby_Woo.png", "NARS_morocco.png", "NARS_Dragon_Girl.png", "PatMcGrath_Elson4.png",
"Sephora_always_red.png", "Tatcha_Kyoto_Red.png", "Gucci_Velvet_Eadie_Scarlet.png",
"PatMcGrath_Blood_Lust.png", "TomFord_flame.png", "Armani_red_to_go.png" ))
# These files were created by copying various photos of TS, cropping rectangle of lips, then
# using https://www.remove.bg/ to remove backgrounds
file = c("ts1_lips-removebg-preview.png", "ts2_lips-removebg-preview.png",
"ts3_lips-removebg-preview.png", "ts4_lips-removebg-preview.png","ts5_lips-removebg-preview.png")
name = c("TS photo 1", "TS photo 2", "TS photo 3", "TS photo 4" ,"TS photo 5")
df_photos <- data.frame(file, name)
############
# p10 for ten lipstick shades, but some only have 1 color
p10 <- function(image, name) {
# Get primary color
primary_color <- colouR::getTopCol(image, n = 1, avgCols = FALSE, exclude = TRUE)
top10 <- tryCatch(
{
colouR::getTopCol(image, n = 10, avgCols = FALSE, exclude = TRUE)
},
error = function(e) {
primary_color
}
)
if (nrow(top10) < 10) {
top10 <- rbind(top10, top10[rep(1, 10 - nrow(top10)),])
}
plot <- ggplot(top10, aes(x = hex, y = freq, fill = hex)) +
geom_bar(stat = 'identity') +
scale_fill_manual(values = top10$hex) +
labs(title = paste(name, "Top 10 colors by frequency")) +
xlab("HEX color code") + ylab("Frequency") +
theme(
legend.position = "none",
plot.title = element_text(size = 15, face = "bold"),
axis.title = element_text(size = 15, face = "bold"),
axis.text.x = element_text(angle = 45, hjust = 1, size = 12, face = "bold")
)
print(plot)
return(top10)
} # close p function
shade_dataframe <- data.frame(matrix(ncol = 10, nrow = 0))
for (i in 1:10) {
result <- p10(df_lipsticks$file[i], df_lipsticks$shade[i])
# Repeat the first color if there are fewer than 10 colors
if (nrow(result) < 10) {
result <- rbind(result, result[rep(1, 10 - nrow(result)),])
}
shade_dataframe <- rbind(shade_dataframe, t(result$hex))
}
colnames(shade_dataframe) <- paste0("Color", 1:10)
print(shade_dataframe)
#############
p5 <- function(image, name) {
top10 <- colouR::getTopCol(image, n = 10, avgCols = FALSE, exclude = TRUE)
return(top10)
}
df_ts_colors <- data.frame()
for(i in 1:nrow(df_photos)){
top10_colors <- p5(df_photos$file[i], df_photos$name[i])
top10_colors <- top10_colors$hex
df_ts_colors <- if(i == 1) {
df_ts_colors <- top10_colors
} else {rbind(df_ts_colors, top10_colors)
}
}
colnames(df_ts_colors) <- c("color1","color2","color3","color4","color5",
"color6","color7","color8","color9","color10")
rownames(df_ts_colors) <- df_photos$name
df_ts_colors <- t(df_ts_colors)
print(df_ts_colors)
# begin total RGB distance of a TS photo to centroid of lipstick shade
# sample 3d plot
library(scatterplot3d)
m <- data.frame(
x = c(174,134),
y = c(31,26),
z = c(61,35))
s3d <- scatterplot3d(m$x, m$y, m$z, pch = 19, color = "blue",
xlim = c(100, 200), ylim = c(0, 50), zlim = c(0, 100),
xlab = expression(bold("R-axis")), ylab = expression(bold("G-axis")), zlab = expression(bold("B-axis")),
main = "Plot of two colors in RGB space", cex.main = 2)
s3d$points3d(m$x, m$y, m$z, type = "l", lty = 1, lwd = 2, col = "red")
# Use 'text' for adding labels with bold font
text(s3d$xyz.convert(m$x, m$y, m$z), labels = paste0("(", m$x, ",", m$y, ",", m$z, ")"),
pos = 3, cex = 2, col = "#00008B", font = 2)
A <- shade_dataframe$Color1
B <- shade_dataframe$Color2
C <- shade_dataframe$Color3
D <- shade_dataframe$Color4
E <- shade_dataframe$Color5
F <- shade_dataframe$Color6
G <- shade_dataframe$Color7
H <- shade_dataframe$Color8
I <- shade_dataframe$Color9
J <- shade_dataframe$Color10
hex_to_rgb <- function(hex) {
rgb <- t(col2rgb(hex))
return(data.frame(r=rgb[1,], g=rgb[2,], b=rgb[3,]))
}
# Function to calculate Euclidean distance between two RGB vectors
euclidean_distance <- function(rgb1, rgb2) {
sqrt(sum((rgb1 - rgb2)^2))
}
# Function to calculate centroid of a vector of hex colors
calculate_centroid <- function(hex_colors) {
rgb_values <- hex_to_rgb(hex_colors)
centroid <- colMeans(rgb_values)
return(centroid)
}
# Calculate centroids of shades, e.g., centroid_A <- calculate_centroid(A)
centroids <- lapply(list(A, B, C, D, E, F, G, H, I, J), calculate_centroid)
for (j in 1:nrow(df_photos)) {
x <- df_ts_colors[,j]
centroid_x <- calculate_centroid(x)
# Calculate total distance of x to each centroid
total_distance_to_centroid <- function(x, centroid) {
x_rgb <- hex_to_rgb(x)
total <- 0
for (i in 1:nrow(x_rgb)) {
total <- total + euclidean_distance(x_rgb[i, ], centroid)
}
return(total)
}
distances <- sapply(centroids, total_distance_to_centroid, x = x)
w <- which(distances == min(distances))
most_similar <- shade[w]
cat("The lipstick most similar to", df_photos$name[j], "is:", most_similar,
"with distance of ", min(distances), "\n")
} # end for loop on photos
# END
file 3 of 3: lyrics.txt
library(taylor)
library(dplyr)
library(tidyverse)
library(tidytext)
data(stop_words)
library(textclean)
library(SnowballC) # For stemming
library(textstem) # For lemmatization
######################################
# functions, preliminaries
# function to print more rows
more_rows <- function(filename){
options(tibble.print_max = nrow(filename), tibble.print_min = nrow(filename))
print(filename)
}
# function to fix informal speech (colloquialisms); also contractions, punctuation, lower case
colloq <- function(df) {
pattern <- "ahh|Ah-uh|ahah|eh|haah|haha|iiii|Oh|oh|Oh-oh|oh-oh|ooh-oh|oohah|Uh|Uh-oh|uh-oh-oh-oh|ya|La-la-la|lala|la-la-la|la-la-la-la|Mm-mm|Mmm-mm|mm-mm|mm-mm-mm-mm|Ha-ha-ha"
df <- df %>%
mutate(lyric = str_remove_all(lyric, paste0("\\b(", pattern, ")\\b"))) %>%
mutate(lyric = str_replace_all(lyric,
c("ain't" = "is not",
"Beggin'" = "begging", "beggin'" = "begging", "birth right" = "birthright", "blood-soaked" = "blood soaked",
"'bout" = "about", "burnin'" = "burning", "callin'" = "calling", "'Cause" = "because", "'cause" = "because", "Cept" = "Except", "cursee" = "cure",
"convers" = "conversation","crashin'" = "crashing", "doin'" = "doing", "driftin'" = "drifting", "dyin'" = "dying", "'em" = "them", "feelin'" = "feeling", "flyin'" = "flying","feverishlying" = "feverishly", "'fore" = "before", "'Fore" = "before", "foreyesgn" = "foreign",
"everythi-i-ing" = "everything","fuckin'"="fuck", "gettin'" = "getting", "gonna" = "going to", "gotta" = "got to", "happ'nin'" = "happening", "haven't" = "have not", "Holdin'" = "holding", "hero's" = "hero",
"Hopin'" = "hoping", "hopin'" = "hoping","I'ma" = "I am going to", "kinda"="kind of", "king's" = "king", "keepin" = "keeping", "Laughin'" = "laughing", "lookin'" = "looking", "losin" = "losing", "losingg" = "losing", "lovin'" = "loving", "lucki" = "lucky", "no-one" = "no one", "Nothin'" = "nothing", "nothin'" = "nothing","one-hand" = "one hand",
"mornin'" = "morning", "'nother"="another", "nothin'" = "nothing", "pickin'" = "picking", "post-mortem" = "postmortem", "prayin'" = "praying", "Prayin'" = "praying", "pretti" = "pretty", "ridin'" = "riding", "Sneakin'" = "sneaking",
"outta" = "out of", "'round" = "around", "self-implode" = "self implode", "shoulda" = "should have", "standin'" = "standing", "summer's" = "summer is", "There's" = "there is", "Thinkin'" = "thinking",
"thankin'" = "thanking", "thinkin'" = "thinking", "'Til" = "until", "'til" = "until", "tryin'" = "trying", "tryna" = "trying to", "Tryna" = "trying to","twin-sized" = "twin sized",
"waitin'" = "waiting", "white-knuckle" = "white knuckle",
"wanna" = "want to", "weepin'" = "weeping", "whatcha" = "what are you", "Where's" = "where is", "Why'd" = "why did",
"wide-eyed" = "wide eyed", "wonderin'" = "wondering", "Wonderin'" = "wondering"))) %>%
mutate(lyric = map_chr(lyric, clean_text))
return(df)
}
custom_stop_words <- bind_rows(stop_words,
tibble(word = c("ah", "dadadada", "ha", "haha", "hey", "hi", "huh", "la", "MMM", "mmm", "mmmm", "mm", "na", "oh", "okay","OK", "ok", "ooh",
"uh", "whoa", "woah", "yeah"), lexicon = "custom"))
# Function to clean text (included in colloq function)
clean_text <- function(text) {
text %>%
replace_contraction() %>%
str_remove_all("[[:punct:]]") %>%
str_to_lower()
}
replacements_df <- read.csv("my_path/lem_replacements_df.csv", header = TRUE)
# Function to stem and lemmatize
pro <- function(words_df) {
words_df <- words_df %>% filter(!is.na(word))
processed_words <- words_df %>%
mutate(stemmed_word = wordStem(word),
lemmatized_word = lemmatize_words(stemmed_word)) %>%
filter(lemmatized_word != "") %>% # Filter out empty strings
left_join(replacements_df, by = c("lemmatized_word" = "stemmed_word")) %>%
mutate(lemmatized_word = ifelse(is.na(lemmatized_word.y), lemmatized_word, lemmatized_word.y)) %>%
select(-lemmatized_word.y) # Remove the extra column created during the join
}
nrc_sentiments <- get_sentiments("nrc") %>%
filter(word != "count" & word != "heel" & word != "truck" & word != "wear" & word != "word")
common_theme <- theme(
legend.position="NULL",
plot.title = element_text(size = 15, face = "bold"),
plot.subtitle = element_text(size = 12.5, face = "bold"),
axis.title = element_text(size = 15, face = "bold"),
axis.text = element_text(size = 15, face = "bold"),
legend.title = element_text(size = 15, face = "bold"),
legend.text = element_text(size = 15, face = "bold"))
sentiment_colors <- c("anger" = "red", "anticipation" = "green", "disgust" = "brown",
"fear" = "purple", "joy" = "yellow", "negative" = "gray", "positive" = "lightblue",
"sadness" = "blue", "surprise" = "pink", "trust" = "turquoise")
emotion_plot <- function(sentiment_summary, song, r){
ggplot(sentiment_summary, aes(x = sentiment, y = word_count, fill = sentiment)) +
geom_col(color = "black") +
scale_fill_manual(values = sentiment_colors) +
labs(title = paste(song, "# words by emotion"),
subtitle = paste("emotional words / all (processed) words =", r),
x = "Emotion",
y = "Number of Words") +
common_theme +
theme(axis.text.x = element_text(angle = 45, hjust=1))
}
lemmatized_colors <- c("red", "blue", "green", "orange",
"purple", "cyan", "magenta", "yellow", "brown", "pink")
word_plot <- function(word_summary, song, title){
ggplot(word_summary, aes(x = lemmatized_word, y = total_count, fill = lemmatized_word)) +
geom_col(color = "black") +
scale_fill_manual(values = lemmatized_colors) +
labs(title = paste(song, title),
x = "",
y = "Frequency") +
common_theme +
theme(axis.text.x = element_text(angle = 45, hjust=1))
}
all_albums <- c("Taylor Swift", "Fearless (Taylor's Version)", "Speak Now (Taylor's Version)", "Red (Taylor's Version)", "1989 (Taylor's Version)",
"reputation", "Lover", "folklore", "evermore", "Midnights", "THE TORTURED POETS DEPARTMENT")
number_of_tracks <- c(15, 26, 22, 30, 22, 15, 18, 17, 17, 19, 31)
original_release_year <- c(2006, 2008, 2010, 2012, 2014, 2017, 2019, 2020, 2020, 2022, 2024)
# The years are original release years, i.e., not "Taylor's version" years
#######################################
# Find song by word in title - could be lower case!
x <- "ricochet"
df1 <- taylor_album_songs %>%
select(album_name, track_name) %>%
filter(grepl(x, track_name))
n <- df1$album_name[1]
a <- which(all_albums == n)
a
# Find track number
x <- df1$track_name[1]
t <- taylor_album_songs %>%
filter(album_name == n) %>%
select(album_name, track_number, track_name) %>%
filter(track_name == x) %>%
select(track_number) %>%
pull() %>% as.numeric()
t
Or instead, choose album a & track t eg: Style: a=11, t=3
# a <- 8
# t <- 5
#######################################
song <- taylor_album_songs %>%
# filter(album_name == all_albums[a] ) %>% # all songs in an album
filter(album_name == all_albums[a] & track_number == t) %>%
pull(track_name[1]) # NOTE the track_name is always 1
if (length(song) == 0) print("No such track number/song") else print(song)
song <- gsub("\\(Taylor's Version\\)|\\[Taylor's Version\\]", '', song)
album <- all_albums[a]
df <- taylor_album_songs %>%
filter(album_name == all_albums[a] & track_number == t) %>%
select(lyrics) %>%
unnest(lyrics) %>%
select(line, lyric)
more_rows(df) # Examine for colloquialisms; add to function colloq
df <- colloq(df)
more_rows(df)
words_df <- df %>%
unnest_tokens(word, lyric) %>%
anti_join(custom_stop_words, by = "word")
more_rows(words_df)
processed_words <- pro(words_df)
more_rows(processed_words) # Examine for words incorrectly lemmatized; add to function pro
processed_words_count <- processed_words %>%
select(lemmatized_word) %>%
group_by(lemmatized_word) %>%
summarize(total_count = n()) %>%
arrange(desc(total_count)) %>%
head(10)
more_rows(processed_words_count)
total_processed_words <- nrow(processed_words)
sentiment_analysis <- processed_words %>%
inner_join(nrc_sentiments, by = c("lemmatized_word" = "word"),
relationship = "many-to-many") %>%
count(lemmatized_word, sentiment, sort = TRUE)
distinct_sentiment_words <- sentiment_analysis %>%
pull(lemmatized_word) %>%
n_distinct()
total_sentiment_words <- sentiment_analysis %>%
select(lemmatized_word, n) %>%
distinct() %>%
group_by(lemmatized_word) %>%
summarize(total_count = sum(n)) %>%
summarize(total_count = sum(total_count)) %>%
pull(total_count)
r <- round(total_sentiment_words / total_processed_words, 3)
cat("emotional words = ", total_sentiment_words, ", total processed words = ", total_processed_words, ", ratio = ", r )
sentiment_summary <- sentiment_analysis %>%
group_by(sentiment) %>%
summarise(word_count = sum(n))
sentiment_summary
word_summary <- sentiment_analysis %>%
select(lemmatized_word, n) %>%
distinct() %>%
group_by(lemmatized_word) %>%
summarize(total_count = sum(n)) %>%
arrange(desc(total_count)) %>%
head(10)
word_summary # check for word with unusual sentiment (truck = trust?); delete from NRC
word_plot(processed_words_count, song,
title="10 most frequent processed words")
word_plot(word_summary, song,
title = "10 most frequent emotional words")
emotion_plot(sentiment_summary, song, r)
# End individual song analysis; for all songs combined, in df <- taylor_album_songs %>%
# delete filter(album_name == all_albums[a] & track_number == t) %>%, and also song <- ""
dirty_words <- processed_words %>%
select(lemmatized_word) %>%
filter(, lemmatized_word=="fuck" | lemmatized_word=="shit" | lemmatized_word=="slut" | lemmatized_word=="bitch") %>%
group_by(lemmatized_word) %>%
mutate(lemmatized_word = str_replace(lemmatized_word, "fuck", "f**k")) %>%
mutate(lemmatized_word = str_replace(lemmatized_word, "shit", "sh*t")) %>%
mutate(lemmatized_word = str_replace(lemmatized_word, "slut", "sl*t")) %>%
mutate(lemmatized_word = str_replace(lemmatized_word, "bitch", "b*tch")) %>%
summarize(total_count = n())
dirty_words # limited to these four; there are others :)
dirty_colors <- c("#FF0000","#000000","#800080","#FFA500")
ggplot(dirty_words, aes(x = lemmatized_word, y = total_count, fill = lemmatized_word)) +
geom_col(color = "black") +
scale_fill_manual(values = dirty_colors) +
labs(title = "TS # of R-rated Words",
x = "",
y = "Number of Words") +
common_theme
# END